Definition
Funktionen mit der Funktionsgleichung f(x)=ax^2+bx+c werden quadratische Funktionen genannt. Für a, b und c kannst du jede beliebige reelle Zahl einsetzen, wobei a aber nicht 0 sein darf.
Der Graph einer quadratischen Funktion heißt Parabel. Ihr Scheitelpunkt ist entweder der Hochpunkt oder der Tiefpunkt.
Je nachdem welchen Wert die Parameter a, b und c haben, verändert sich der Verlauf des Graphen. Die folgende Unterteilung baut systematisch aufeinander auf:
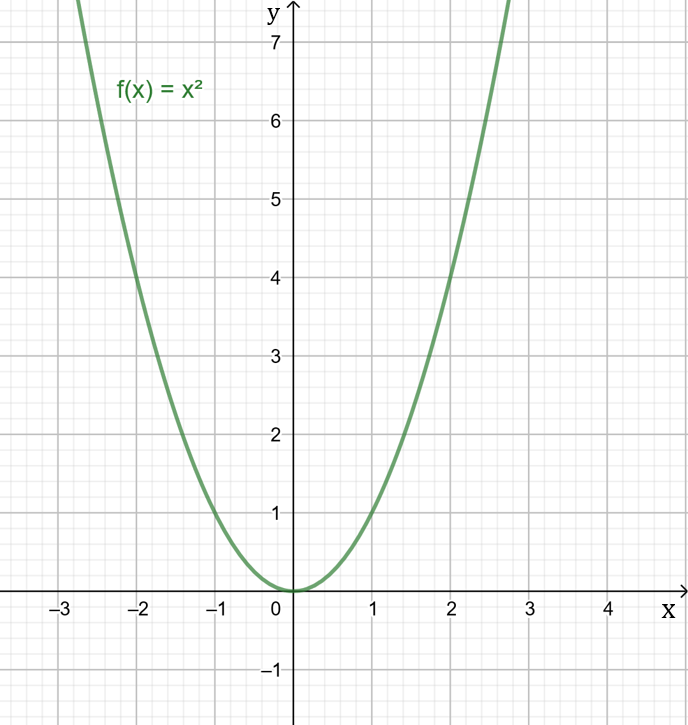
- Normalparabel: f(x)=x^2
- gestreckte/gestauchte Normalparabel, nach oben/unten geöffnet: f(x)=ax^2
- entlang der y-Achse verschobene Parabel: f(x)=ax^2+c
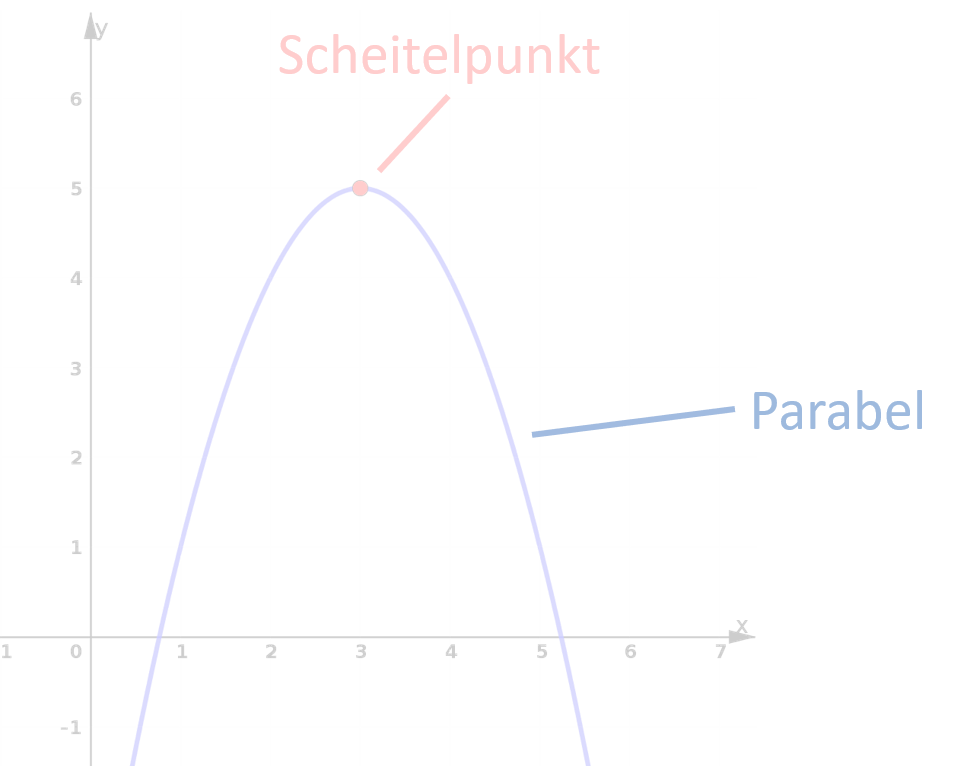
- Scheitelpunktform: f(x)=a(x-d)^2+e
- allgemeine Form: f(x)=ax^2+bx+c
Je nachdem welchen Wert die Parameter a, b und c haben, verändert sich der Verlauf des Graphen. Die folgende Unterteilung baut systematisch aufeinander auf:
- Normalparabel:
f(x)=x^2 - gestreckte/gestauchte Normalparabel, nach oben oder nach unten geöffnet:
f(x)=ax^2 - auf der y-Achse verschobene Normalparabel:
f(x)=ax^2+c - Scheitelpunktform:
f(x)=a(x-d)^2+e - allgemeine Form:
f(x)=ax^2+bx+c
Normalparabel
Die einfachste Form einer quadratischen Funktion lautet: f(x)=x^2. Sie wird auch Quadratfunktion genannt. Ihr Scheitelpunkt liegt bei (0|0). Ihr Graph heißt Normalparabel.
Du kennst bereits die Quadratzahlen, also positive, ganze Zahlen, die mit sich selbst multipliziert werden, z. B.:
\begin{aligned}5^2&=5\cdot 5=25 \\ 2^2&=2\cdot 2=4\end{aligned}
Die Quadratfunktion macht genau das Gleiche, nur für beliebige reelle Zahlen.\begin{aligned}f(0.5)&=0.5^2=0.5\cdot 0.5=0.25 \\ f(-2)&=(-2)^2=(-2)\cdot (-2)=4\end{aligned}
Über eine Wertetabelle kannst du für viele verschiedene Zahlen die Funktionswerte berechnen. Dafür setzt du für x konkrete reelle Zahlen in die Funktionsgleichung und berechnest y. Das entstandene Wertepaar aus x und y steht stellvertretend für einen Punkt P(x|y) des Graphen im Koordinatensystem.| \mathbf{x} | \mathbf{y=f(x)=x^2} |
|---|---|
| -3 | (-3)^2=9 |
| -2 | (-2)^2=4 |
| -1 | (-1)^2=1 |
| -0.5 | (-0.5)^2=0.25 |
| 0 | 0^2=0 |
| 0.5 | (0.5)^2=0.25 |
| 1 | 1^2=1 |
| 2 | 2^2=4 |
| 3 | 3^2=9 |
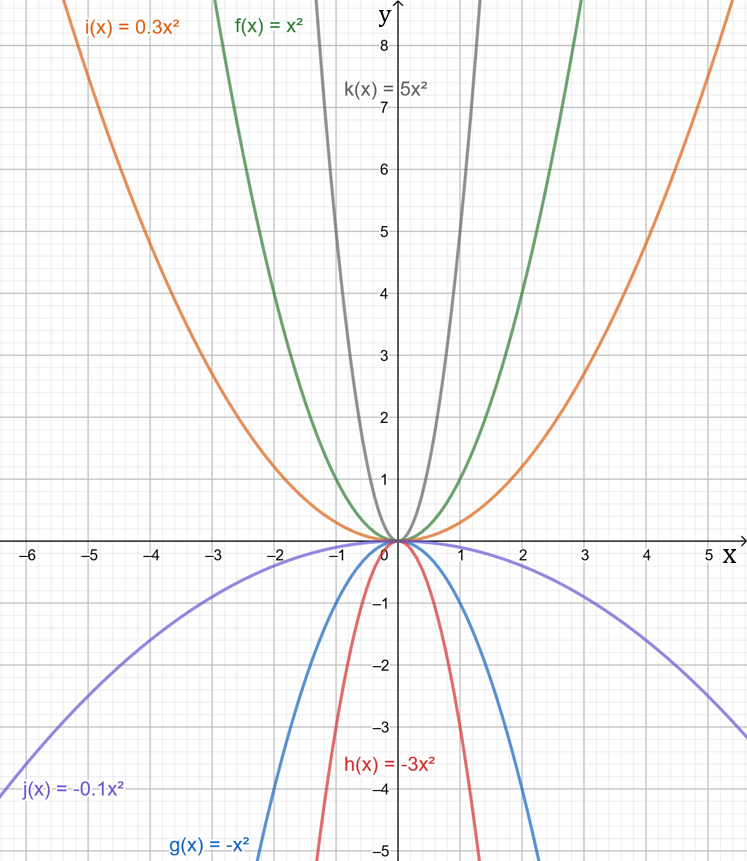
gestreckte oder gestauchte Normalparabel, nach oben oder nach unten geöffnet
Die quadratische Funktion der Form f(x)=ax^2 unterscheidet sich im Verlauf des Graphen zur Normalparabel f(x)=x^2. Dafür ist der Parameter a verantwortlich, der heißt Streckfaktor heißt. Der Scheitelpunkt liegt aber immernoch bei (0|0).
Es gibt grundsätzlich vier verschiedene Möglichkeiten, den Parameter a zu besetzen und so den Verlauf des Graphen zu verändern.
- a>0 → Parabel nach oben geöffnet
- a<0 → Parabel nach unten geöffnet
- |a|>1 → Parabel gestreckt, also enger
- |a|<1 → Parabel gestaucht, also weiter
Auch hier hast du natürlich die Möglichkeit, eine Wertetabelle aufzustellen. Beachte aber, dass du den Parameter a nicht ungewollt mitzuquadrierst. Vergleiche am Graphen der Funktion j:
\begin{aligned}j(x)&=-0.1x \\ j(2)&=-0.1\cdot 2^2=-0.1\cdot 4=-0.4 \\ j(-3)&=-0.1\cdot (-3)^2=-0.1\cdot 9=-0.9\end{aligned}
entlang der y-Achse verschobene Parabel
Die quadratische Funktion der Form f(x)=ax^2+c ist gegenüber dem Graphen der quadratischen Funktion f(x)=ax^2 um den Parameter c längs der y-Achse verschoben. Ihr Scheitelpunkt liegt auf der y-Achse im Punkt (0|c). Für den Parameter a gelten weiterhin die Änderungsbedingungen für gestreckte/gestauchte bzw. nach oben/unten geöffnete Normalparabeln.
Scheitelpunktform
Die quadratische Funktion der Form f(x)=a(x-d)^2+e heißt Scheitelpunktform. Der Scheitelpunkt dieser Parabel liegt bei (+d|e). Du kannst ihn sofort ablesen. Achte aber auf den Vorzeichenwechsel. Bei f(x)=a(x+d)^2+e ist der Scheitelpunkt (-d|e). Der Parameter a sorgt für die Formänderung der Parabel.
Durch Ausmultiplizieren der Scheitelpunktform lässt sich die allgemeine Form erzeugen.
\begin{aligned}f(x)&=a(x-d)^2+e \\ &=a(x^2-2dex+d^2)+e \\ &=ax^2-2adex+ad^2+e\quad|2ade=b\quad ad^2+e=c \\ &=ax^2-bx+c\end{aligned}
allgemeine Form
Die allgemeine Form einer quadratische Funktion lautet f(x)=ax^2+bx+c. Der Parameter c bestimmt den y-Achsenabschnitt, also die Stelle, an der der Graph die y-Achse schneidet. Der Parameter a verändert die Form der Parabel (nach oben/unten geöffnet bzw. gestreckt/gestaucht).
quadratische Ergänzung
Über die quadratische Ergänzung kann die allgemeine Form f(x)=ax^2+bx+c zur Scheitelpunktform f(x)=a(x-d)^2+e umgewandelt und dann der Scheitelpunkt abgelesen werden. Für euch ist nur die reduzierte Variante relevant, d. h. es gilt a=1.
Nullstellen
Die Schnittpunkte einer Funktion mit der x-Achse werden Nullstelle genannt. Die y-Koordinate dieses Punktes ist also 0. (Schreibweise: S_x(x_0|0), wobei x_0 die x-Koordinate des Punktes ist, der auf der x-Achse liegt). Die notwendige Bedingung für das Vorliegen einer oder mehrerer Nullstellen lautet y=f(x_0)=0.
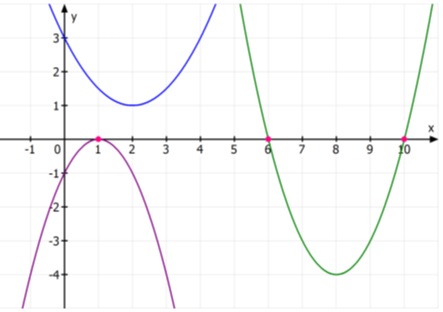
Bei quadratischen Funktion gibt es je nach Lage und Form der Parabel also drei verschiedene Möglichkeiten für die Existenz von Nullstellen.
- keine Nullstelle (Scheitelpunkt oberhalb der x-Achse und Parabel nach oben geöffnet bzw. Scheitelpunkt unterhalb der x-Achse und Parabel nach unten geöffnet)
- eine Nullstelle (Scheitelpunkt liegt exakt auf der x-Achse)
- zwei Nullstellen (Scheitelpunkt oberhalb der x-Achse und Parabel nach unten geöffnet bzw. Scheitelpunkt unterhalb der x-Achse und Parabel nach oben geöffnet)
interaktive Übungen
